Voronoi tessellation-based mesh generator for the mesoscale structure of wood

Wood has a unique micromorphology featuring a local pattern of prismatic cells and a global pattern of annual growth rings. Understanding the role of locally irregular and globally radial micromorphology in determining material properties offers a new path to unveil the behavior of wood and wood-based materials with functionalities, such as anisotropic material properties, stress redirection, and oriented impact energy dissipation. While laboratory and in-situ imaging approaches are reliable for the reconstruction of high-resolution wood micromorphologies in computational modeling, algorithm-based generation of wood microstructure geometries are still in high demand. They have the advantage of lowering cost while enabling rapid prototyping and stochastic analysis of wood products during the design phase. This study develops a rapid wood micromorphology modeling technique, based on Voronoi tessellation and Lloyd's relaxation algorithm, to mimic the prismatic cellular microstructure for softwood in 3D. The generated wood microstructure is then integrated with the Connector-Beam Lattice Model for wood (CBL-W) to establish a pipeline for numerical simulations of the quasi-static and fracture properties of wood and wood-based materials.

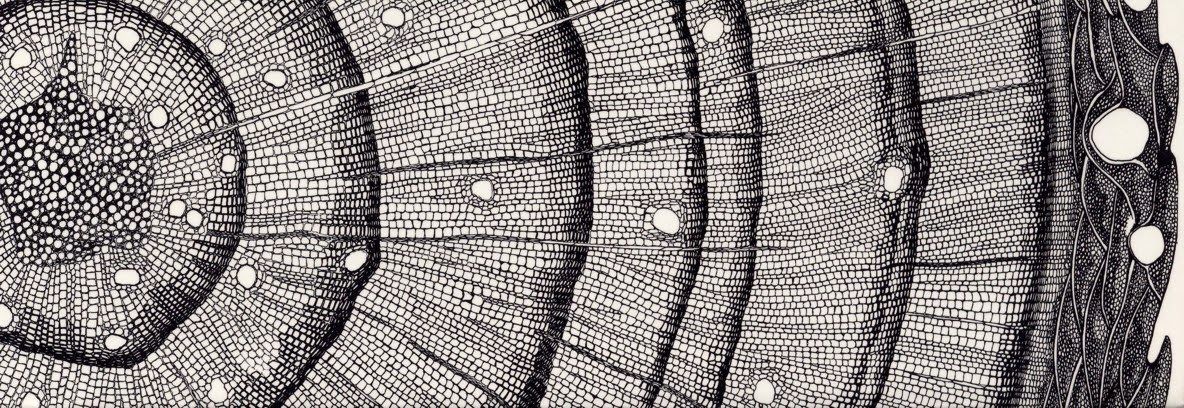
Image credit: Fritts, Harold. Tree rings and climate. Elsevier, 2012.

Multiscale structure of wood

Wood and engineered wood composites are biological composite materials that are made up of several hierarchical levels of organization. They have different structures at different levels of scale, from the macroscopic to the microscopic.

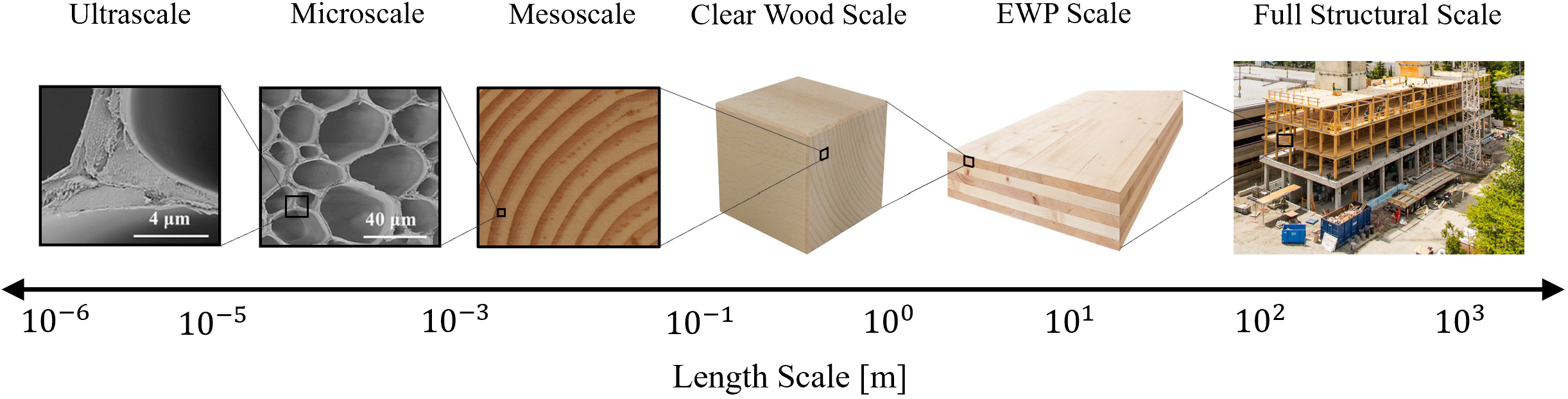
At the macroscopic level, wood has a complex structure of annual growth rings, which are formed as a result of variations in the rate of growth of the tree over the course of a year. The growth rings are composed of concentric layers of wood, each with its own distinct properties, such as density, porosity, and strength.

At the mesoscopic level, wood has a cellular structure that consists of longitudinal cells called tracheids and fibers, which are responsible for the mechanical strength and flexibility of the material. These cells are arranged in layers in the longitudinal direction, which give wood its characteristic grain pattern.

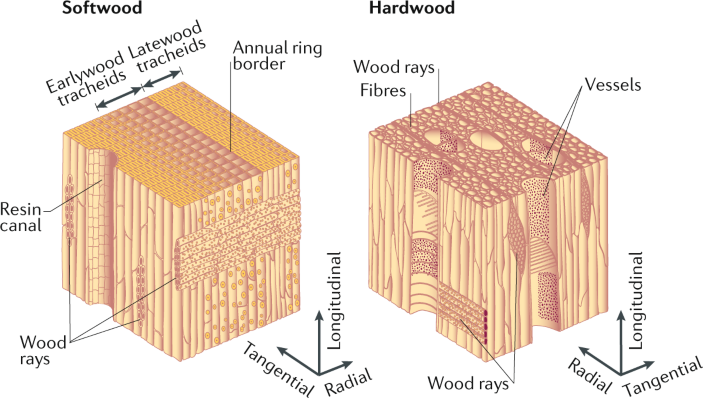
Image credit: Chen, Chaoji, et al. "Structure–property–function relationships of natural and engineered wood." Nature Reviews Materials 5.9 (2020): 642-666.

At the microscopic level, wood is composed of cellulose fibers that are arranged in a helical pattern, surrounded by a matrix of lignin and other compounds. The arrangement of these fibers gives wood its unique mechanical properties, including high stiffness and strength, as well as the ability to withstand bending and compression.

In this project, we focus on the mesoscale structure of wood, at which the solid constituents (i.e., tracheids and fibers) exhibit the "intrinsic heterogeneity and anisotropy" of the material at the µm level.

Voronoi tessellation for wood mesostructure

The cellular mesostructure of wood is a natural outcome of local cell growth that follows simple intrinsic physical rules, among these, Voronoi diagram (Voronoi diagram - Wikipedia), has been proposed to be one of the simple but accurate approximations of cell interfaces at the steady-state by the equilibrium of intracellular pressures and the intercellular surface tension in a plane. This Voronoi diagram is also suitable for representing sections of other cellular materials, such as trabecular bone, skeletal muscle fiber and some 3D printed biomimetic composites.

Image credit: Parametric House

To generate a 2D Voronoi diagram for wood section, we firstly pick a set of input points (a.k.a., seeds), which will determine the Voronoi cells and follows rules such as the wood cell density distribution. Then for each input point, we determine the set of points that are closest to it. These points form the boundary of the Voronoi cell for that input point. We then connect adjacent Voronoi cells to form the edges of the diagram, these edges represent wood cell walls. In some cases, the Voronoi cells may extend infinitely far in one or more direction, these infinite cells combined with the finite cells on the boundary lines of the model are truncated and trimed.

Apart from the basic Voronoi diagram, another technique is adopted to achieve a more realistic wood cellular structure: Lloyd's relaxation, also known as Lloyd's algorithm or Voronoi iteration, is a computational method for finding an optimal set of points that minimize the distance between the points and a given set of data. The algorithm iteratively partitions the data space into cells by computing Voronoi diagrams and then moves the points to the centroid of each cell. This process is repeated until convergence, which means that the point set no longer changes significantly. By using Lloyd's relaxation with appropriate boundary conditions, we can simulate the radial growth process of wood cells. One example of the simulation of softwood growth is as shown in figure below:

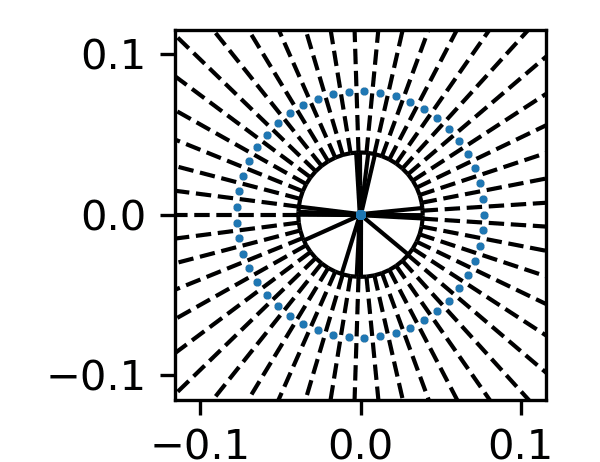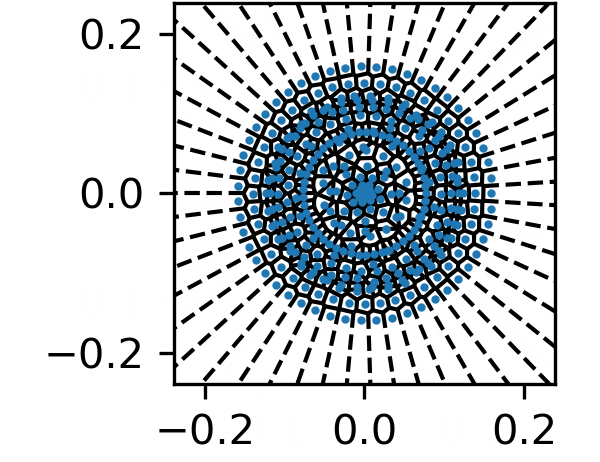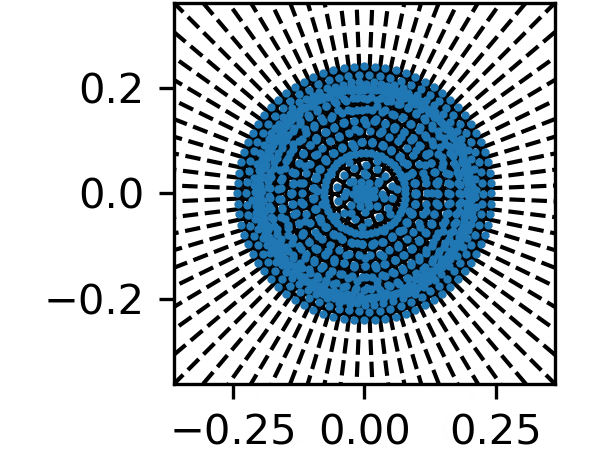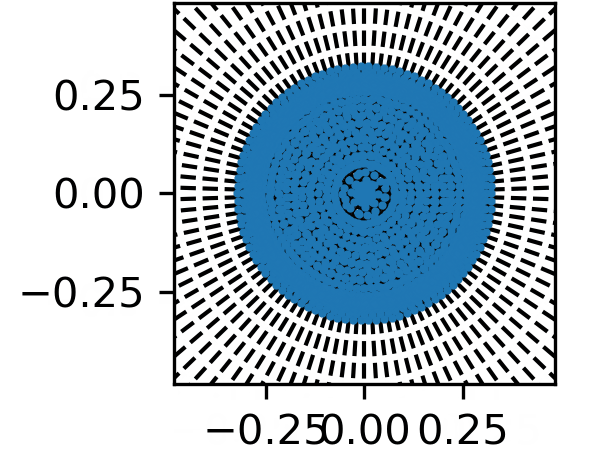
The formation of the annual growth rings follows density models of annual rings. We firstly employ a truncated normal distribution for the annual ring widths, then within each annual ring, the variability of wood cell density is considered via the transition from early wood (larger cell size but smaller cellwall thickness) to late wood (smaller cell size but larger cellwall thickness).

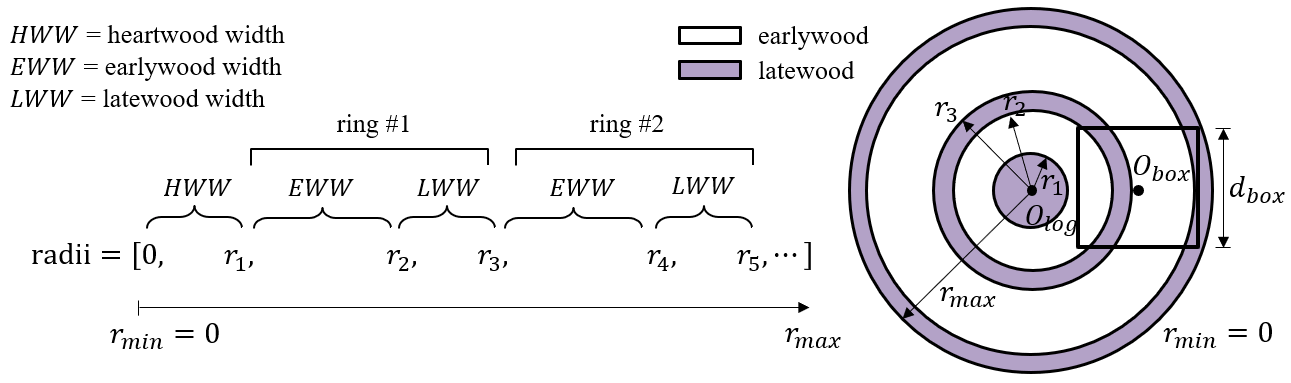
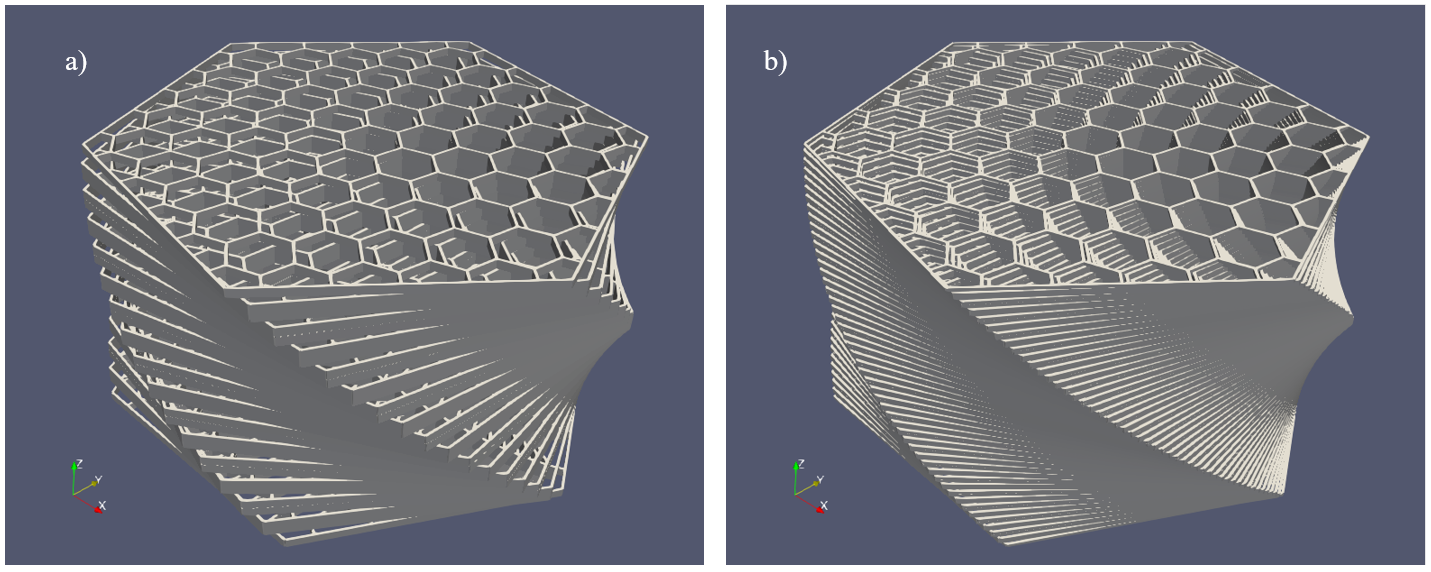
The 2D Voronoi diagram is then rotated and extruded in the longitudinal (out-of-plane) direction, to form the straw-like shapes of wood tracheids or fibers. The extrusion in the longitudinal direction can be cut into many layers, the segments have various lengths which are dependent on the wood species. The rotation angle of wood tracheids or fibers during the extrusion represents the natural inclination during tree growth. The video below illustrates the whole process of longitudinal extrusion, and boundary formation:

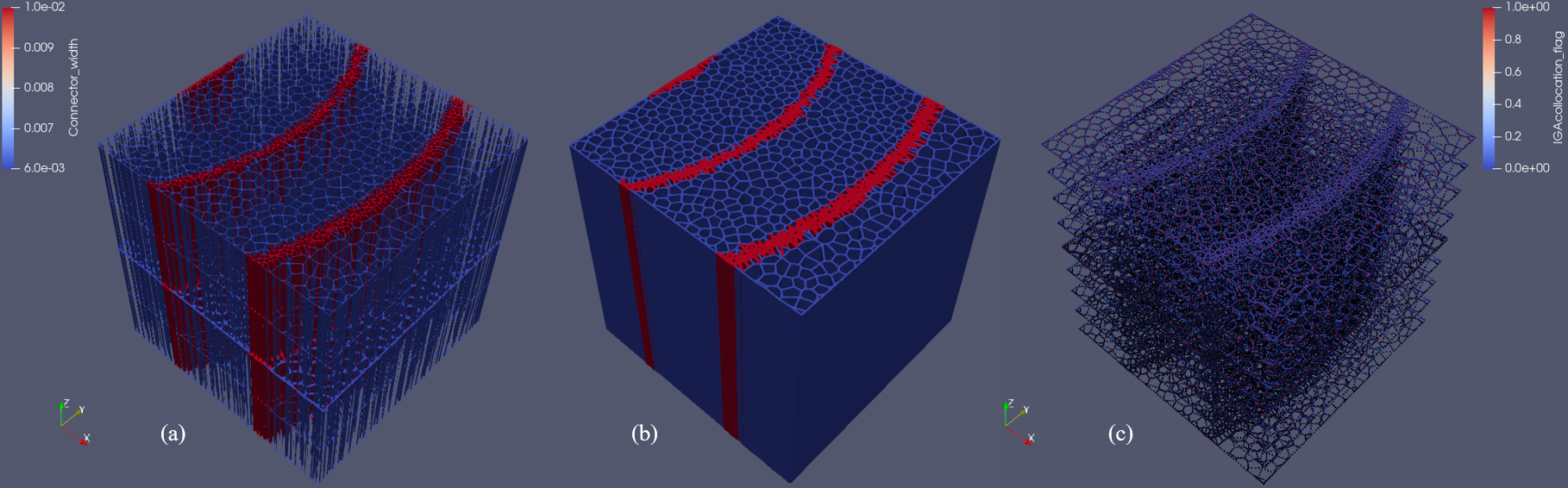
After edge clipping and trimming, the mesh information for the 3D wood mesostructure is stored in a data structure called "connector-beam" system. In this system, we first form a point cloud which contains the featured positions (e.g., boundary, mid point, etc.) of the model, then many of these points are connected to establish a connectivity and geometry data representing the wood tracheids or fibers in 3D, this is so-called "beam" data.

Neighboring beams are then inter-connected by "connectors", and these "connectors" can represent the cell walls if assigned with corresponding geometric properties such as cell wall thicknesses and segment heights. Once we have the connectivity data for "beams" and "connectors", after determining the association relationship between "beams" and "connectors", we can finally establish a 3D model, which contains the information for every single wood tracheid or fiber and the connection.

A examplar 3D model of wood mesostructure is like what is shown in figure below (notched tensile test sample provided by our colleagues from the University of Maine):

RingsPy package for wood micromorphology modeling

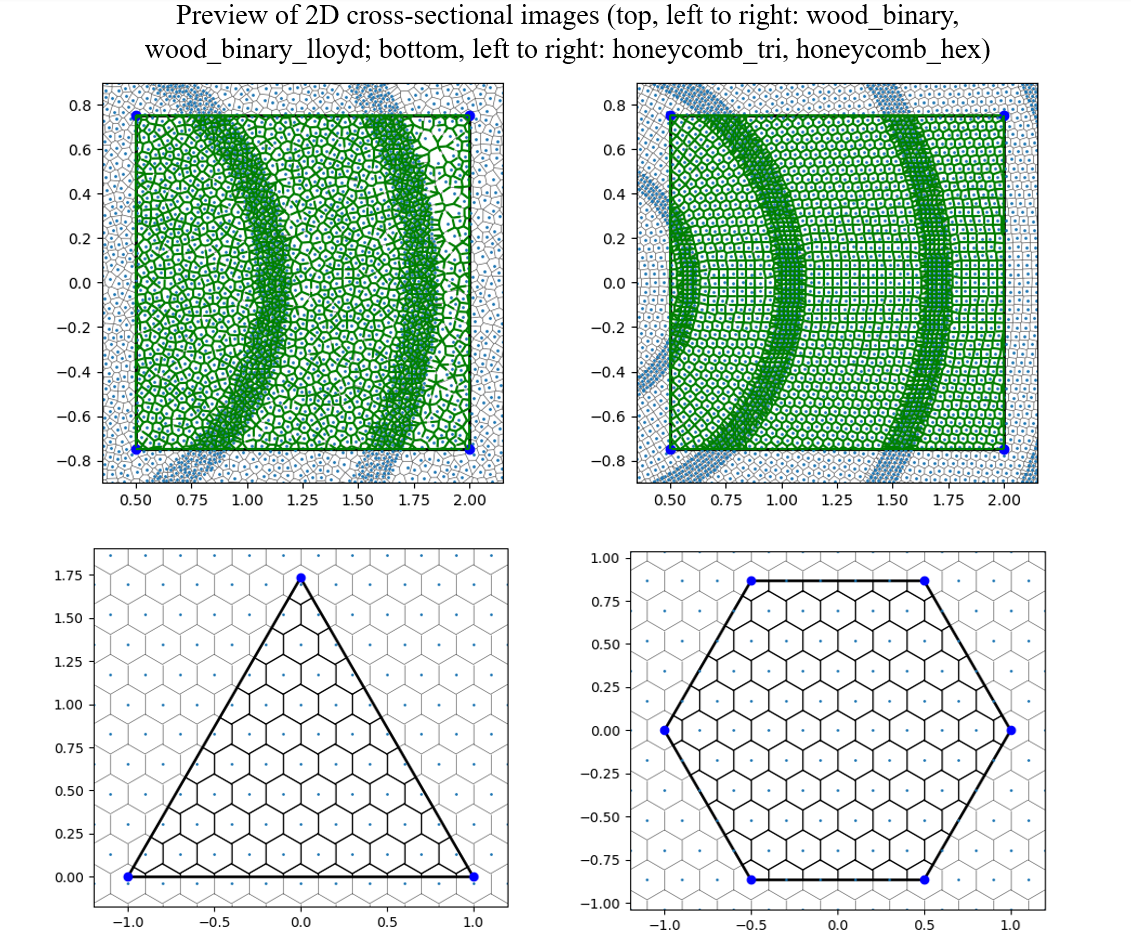
RingsPy (https://github.com/kingyin3613/ringspy) is our open-source package entirely written in Python that generates 3D meshes of prismatic cellular solids with tunable radial growth rules featured by many natural or architectured cellular solids with a radial, differential cell growth pattern. The 2D geometry of the cellular structure of the solid is first constructed with a 2D Voronoi tessellation, and then the 2D Voronoi cells are extruded in the longitudinal (parallel-to-grain) direction with a certain grain angle around the longitudinal axis. This process is supposed to mimic the morphology and dynamic growth of natural or additively manufactured cellular materials.

The package is dependent only on numpy and scipy for core implementation, however, regular cells (e.g., hexagonal honeycomb structure) option is also provided, with the help of Python package hexalattice. The visualization of the generated geometry is implemented using Python package matplotlib for 2D cross-sectional images, and for 3D models using the VTK or STL format files (which can be then used in scientific visualization tools such as Paraview and for 3D printing).

If this package helps you in building a even cooler software or package, or it helps you in your research on wood, honeycomb structure, or other prismatic cellular solids, we kindly ask that you cite this paper:

@article{ringspy,
    doi = {10.21105/joss.04945},
    url = {https://doi.org/10.21105/joss.04945},
    year = {2023},
    publisher = {The Open Journal},
    volume = {8},
    number = {83},
    pages = {4945},
    author = {Hao Yin and Gianluca Cusatis},
    title = {RingsPy: A Python package for Voronoi mesh generation of cellular solids with radial growth pattern},
    journal = {Journal of Open Source Software}
}